Read-Aloud Accommodations: Effects on Multiple-Choice Reading and Math Items

NCEO Technical Report 31

Published by the National Center on Educational Outcomes

Prepared by:

John Bielinski, Martha Thurlow, James Ysseldyke, Jim Freidebach, and Melodie Freidebach

September 2001

Any or all portions of this document may be reproduced and distributed without prior permission, provided the source is cited as:

Bielinski, J., Thurlow, M., Ysseldyke, J., Freidebach, J., & Freidebach, M. (2001). Read-aloud accommodations: Effects on multiple-choice reading and math items (TechnicalReport 31). Minneapolis, MN: University of Minnesota, National Center on Educational Outcomes. Retrieved [today's date], from the World Wide Web: http://cehd.umn.edu/NCEO/OnlinePubs/Technical31.htm

This report is based on a paper presented at the annual meeting of the National Council of Measurement in Education, Seattle, Washington, April 11, 2001.

Executive Summary

About 50% of students with a disability participate in the Missouri assessment program with one or more testing accommodations. One of the most prevalent and controversial accommodations is an audio presentation of written test material; for instance, having a proctor read the math test items and response options to the student. There is a dearth of empirical evidence that demonstrates how audio presentation of test material, heretofore referred to as the read-aloud accommodation, affects the construct the test was designed measure. This study uses actual test administration data from the Missouri Assessment Program to examine the effect of using the read-aloud accommodation on the characteristics of multiple-choice math and reading test items administered to students in 3rd and 4th grade.

One of the criticisms of using extant data is that it is difficult to isolate the effect of an accommodation because the presence of an accommodation is confounded with other student characteristics as well as other accommodations. In this study we defined four groups to help control for such confounding effects. Group A represented a random sample of non-accommodated students with no disabilities; Group B was a control group of non-accommodated students with no disabilities who were matched in overall test performance to students with a reading disability; Group C represented students whose primary disability was in reading and who took the test without an accommodation; Group D represented students whose primary disability was in reading and who took the test with the read-aloud accommodation.

Differential item function (DIF) analysis was run on the data using BILOG-MG, which compared item difficulty estimates across several groups simultaneously. The item difficulty estimates for Groups B, C, and D were compared to the estimates for Group A to examine DIF. Because an accommodation is considered a way of improving the quality of measurement for students with a disability, it would be expected that the number of DIF items would be greatest for Group C and that there would be few DIF items for Group D. Among the 32 multiple-choice math test items, there was one DIF item for Group C and six DIF items for Group D. Among the 41 multiple-choice reading items, there were 10 DIF items for Group C and 19 DIF items for Group D.

These findings raise some important questions. First, how can we determine who should benefit from an accommodation? It makes sense to assume that students with a reading disability should benefit from a read-aloud accommodation, yet there were fewer DIF items for those students with a reading disability who did not get the accommodation than for those who did. Replication is needed to confirm this result. Second, it would appear that a reading test measures the reading construct differently for students with a reading disability than for students without disabilities, whether or not the students received the read-aloud accommodation. Without the accommodation, 25% of the items were identified as DIF items, and with the accommodation about 50% of the items were identified as DIF items. More research is needed to determine the best ways to measure reading skills for students who struggle with reading.

Overview

States continue to struggle with the best ways to include students with disabilities in state testing programs. The menu of testing options available for students with disabilities includes taking the regular assessment without accommodations, taking the regular assessment with accommodations, or taking a different assessment. Many students with disabilities take the regular assessment under standard conditions, but a large percent take the regular assessment under accommodated conditions (Thurlow, House, Boys, Scott, & Ysseldyke, 2000). Because the validity evidence for a test is usually tied to an administration without accommodations, it is necessary to gather additional validity evidence for test scores obtained under accommodated conditions. With federal legislation requiring states to report disaggregated results for students with disabilities, the need for additional validity evidence is even greater.

In the research literature on test accommodations, the term accommodation refers to that subset of test changes that do not alter the construct the test was designed to measure. Alterations that change the construct of the test are sometimes called modifications, although some states use the term “modification” for changes considered appropriate (Thurlow, & Weiner, 2000). Generally, an accommodation can be defined as an alteration to the standard test conditions that neutralizes extraneous sources of difficulty resulting from an interaction between standard administration and a student’s disability while preserving the measurement goals of the test (Elliott, Kratochwill, McKevitt, Schulte, Marquart, & Mroch, 1999; Phillips, 1994; Tindal, Helwig, & Hollenbeck, 1999; Willingham, Ragosta, Bennett, Braun, Rock, & Powers, 1988). Validation studies are necessary to ascertain the appropriateness of an alteration. Unfortunately, the evidence substantiating the validity of an accommodation is scant, even for some of the most widely used alterations, such as the read-aloud administration of a test.

Two types of validation evidence for testing accommodation can be derived from the definition of test accommodations. One type of evidence is the test score boost. If accommodations remove extraneous sources of difficulty resulting from an undesirable interaction between standard testing conditions and a student’s disability, then a valid accommodation should result in a performance boost for students with that disability. Because a valid accommodation acts only on the interaction between disability and standard testing conditions, it should not result in a test score boost for students without a disability (Phillips, 1994). Such test score boosts represent necessary but insufficient data to conclude that an accommodation is valid.

A valid test accommodation should preserve the measurement goals of the test as well as result in a performance boost. In other words, it should not alter the construct the test was designed to measure. There are several ways to ascertain whether a set of test items measures the same construct for different examinee groups. One way is to apply differential item function analysis, known as DIF. DIF analysis represents a way to compare item characteristics such as item difficulty across groups. Under the notion of DIF, groups are first equated on ability, which is usually estimated by each person’s overall test score. Presumably, if all of the items measure the same construct in the same way for all groups, then each item should be equally difficult across the ability-matched groups. Finding that many of the items display DIF would be an indication that the test is measuring something different across groups.

DIF analysis requires large samples, at least several hundred cases per group. Most experimental studies contain fewer than 100 participants. State testing databases contain thousands of cases, making it possible to conduct DIF analysis. In addition to containing large samples, such databases represent the real-life testing situations. It is essential that test accommodations demonstrate validity in the real testing environment. Extant databases represent a wonderful source of information for ascertaining the validity of testing accommodations in natural settings.

There are some shortcomings to evaluating the validity of testing accommodations using extant data. Foremost is the fact that there may not be naturally occurring appropriate control groups. Students with disabilities who take a test with an accommodation differ from students without disabilities who do not use accommodations in three common ways: (1) they have a disability, (2) they took the test with an accommodation, and (3) as a group their overall performance is usually (but not always) much lower than their peers without disabilities. In DIF studies that do not account for each of these differences, it would not be appropriate to attribute DIF to the presence of an accommodation because the accommodation is confounded with other factors. One possible solution is to define successive groups wherein one group differs from the reference group only in terms of performance, another that differs in terms of performance and presence of a disability, and one that differs in terms of performance, presence of a disability, and presence of an accommodation. Although it is not possible to ensure that these groups differ only in the ways indicated because students are not randomly assigned to groups, the three layers of control groups do make it possible to begin to isolate the effect of the test accommodation on item functioning. However, even if DIF is attributed in this way to the presence of a testing accommodation, one cannot conclude that the accommodation itself is invalid.

There are three possible explanations for why differential item functioning might exist. It may be that the accommodation simply does not do what proponents think it should do. In other words, the accommodation may change the construct that the test was designed to measure. Another possibility is that the accommodation was not appropriately administered. For example, an accommodation that requires a proctor to read math test items may be ineffective because the proctor read the items too quickly. A third possibility is that the accommodation may have been administered to students who do not actually need it. Research on how accommodations decisions are made indicates that the decision makers, members of the IEP team, tend to over-accommodate students (Elliott et al., 1999; Fuchs , Kratochwill, McKevitt, Schulte, Marquart, & Mroch 2000; Fuchs, Eaton, Hamlett, & Karns, 2000). In other words, they use accommodations that have no benefit for the student. Regardless of knowing the reason why, it is still important to ascertain whether accommodated test scores measure the same construct as non-accommodated test scores.

The read-aloud accommodation is one of the most commonly used accommodations (Bielinski, Ysseldyke, Bolt, Friedebach, & Fredebach, 2001). Prior to this study, only two studies of the read-aloud accommodation used test data from an actual statewide administration of an achievement test to evaluate the validity of the accommodation. Both of those studies used structural equation models to evaluate factor invariance between the scores of non-accommodated students and the scores of students receiving the read-aloud accommodation. Tippets and Michaels (1997) studied the effect of the read-aloud accommodation on a reading test and a language usage test. The tests were part of the Maryland School Performance Assessment Program. Pomplun and Omar (2000) studied the effect of the read-aloud accommodation on a math test that was part of the Kansas Assessment Program. Each study reported that the factor structure was the same for the non-accommodated and the accommodated groups. Both studies fitted a two-factor model to the item sets because a two-factor model resulted in a significant improvement in model fit. However, the reality is that scores from these assessments are based on a single latent trait; therefore, their findings cannot be generalized to the scores actually reported in those states.

The method used in this study produces results that demonstrate whether test items function the same under non-accommodated and accommodated conditions when a single latent trait model is used. In this way, the results can indicate the validity of the test scores reported in the assessment system when the scores were obtained under accommodated conditions.

The read-aloud accommodation, as with any accommodation, should result in scores that are more meaningful for students who need the accommodation as compared to the scores obtained by similar students taking the test without the accommodation. Tindal, Heath, Hollenbeck, Almond, and Harniss (1998) emphasized the importance of the area of student need as defined by the student’s Individualized Education Program (IEP) for making the determination about which accommodations to give; students with the same primary IEP area probably have a common need and should be given the same accommodation. In the Tindal et al. (1998) study, the effect of the read-aloud accommodation on the construct validity of a reading and a math test was evaluated by comparing item difficulty invariance across groups. One group included students whose primary IEP area was reading and who received the read-aloud accommodations; another group also had reading as their primary IEP area but did not receive an accommodation; the other two groups consisted of students without disabilities taking the test without an accommodation.

 

Research Questions

Presumably, all students whose primary IEP area is reading should benefit from the read-aloud accommodation. The performance of students with a reading disability not receiving the read-aloud accommodation should be affected by extraneous sources of difficulty that alter item characteristics. Therefore, the item characteristics based on the students who received the accommodation should closely resemble the item characteristics in the comparison group of non-disabled students, whereas the item characteristics for students with a reading IEP not receiving the accommodation should differ markedly from those in the comparison group.

The research questions for this study are based on the preceding rationale. The two specific research questions are:

•    Is item difficulty the same for students receiving the read-aloud accommodation as for non-accommodated students without disabilities?

•    Does item difficulty markedly differ for students who need the read-aloud accommodation, but did not receive it when compared to the non-accommodated students without disabilities?

Method

Participants

This study uses data from the 1998 administration of the Missouri Assessment Program (MAP). All public school students are required to participate in MAP. Students may participate in the program by taking the regular assessments without accommodations, the regular assessments with accommodations, or an alternate assessment. For students with disabilities, the decision about how the student should participate is usually made by the student’s IEP team. The students and their parents are encouraged to participate in the decision process.

When students with disabilities take the test, their test forms are marked to indicate (1) the primary area of their special instruction (e.g., reading, math, behavior), adding with their category of disability. In addition, the accommodations used by students are indicated. The focus of the study is on those students who primarily receive special education services for reading instruction. For each examinee, the proctor indicated the student’s primary IEP instructional area. Only those students for whom the primary instructional area was reading were used in the two special education groups defined below.

In 1998, there were 52,387 third grade students with a valid communications arts (reading) test score, and 66,800 fourth graders with a valid math test score. Students receiving special education services constituted 11.4% (N=5,962) of the population taking the communication arts test, and 12.7% (N=8,491) of the population taking the mathematics test. From these data, four groups of students were defined. Group A represented a random sample of approximately 1000 general education students who took the test without an accommodation. Group B represented a random sample of approximately 1000 general education students who took the test without an accommodation and who were matched in ability to the group of students with an IEP in reading. The selection of the sample of cases for Group B was done so that the distribution of the number-correct scores on the multiple-choice items matched the pooled distribution of the number-correct scores for groups C and D. Group C represented all of the students whose primary IEP instructional area was reading and who took the test without an accommodation. Group D represented all of the students whose primary IEP instructional area was reading and who took the test under the read-aloud accommodation (either alone or in combination with extended time, small group administration, or both). Most of the students receiving the read-aloud accommodation also received extra time and took the test in a small group.

Table 1 is a summary of group performance on the each test measured as the number of the multiple-choice items answered correctly. Groups B, C, and D have similar means and standard deviations on both the reading test and the mathematics test. The mean number-correct score for Group A was about one standard deviation unit greater than the mean score in the other three groups on both tests. The ratio of males to females in groups C and D was about 2 to 1. These are the groups comprised of students with an IEP in reading. This ratio is similar to the ratio of males and females in special education. Additionally, just over 90% of the students in each group had a learning disability (LD). Groups A and B consisted of nearly equal numbers of males and females.

Table 1. Performance and Gender Makeup of Each Group

 

Group
 

Aa
(General Ed. No Accomm.)

Bb
(Low Perf. No Accomm.)

Cc
(IEP No Accomm.)

Dd
(IEP with Accomm.)
Communication Artse

 

 

 

 

                         Mean

31.0

23.0

21.6

23.7

                            SD

7.13

8.05

7.76

7.50

                        N

1002

995

600

661

                  % Female

49

45

34

33

Mathematicsf

 

 

 

 

                         Mean

24.9

19.2

18.9

20.1

                            SD

5.13

6.23

6.34

5.99

                              N

1139

1006

831

1082

                  % Female

49

50

33

32

a general education students taking the test without accommodations
b low performing non-disabled students taking the test without an accommodation
c IEP students taking the test without an accommodation
d IEP students taking the test with the read-aloud accommodation
e highest possible score = 41
f  highest possible score = 32

 

Instruments

The reading and mathematics tests used in the Missouri Assessment Program (MAP) consist of a combination of norm-referenced test items developed by CTB-McGraw/Hill and items developed expressly to measure Missouri’s Show Me Standards. Tests were divided into three sections referred to as sessions. Session 1 consisted of a combination of performance events and constructed response items, Session 2 consisted of only constructed response items, and Session 3 consisted of only multiple-choice items. The Session 3 items were adapted from the Terra Nova™ to meet Missouri’s achievement standards and they are included to provide national normative comparisons. The present study used only the multiple-choice items.

The reading test administered in 3rd grade consisted of 41 multiple-choice items that assess reading comprehension on six reading passages. Passages were either short fictional stories with fewer than 250 words or short poems. Students were required to answer both literal and inferential test items.

The mathematics test that is administered in 4th grade consisted of 32 multiple-choice items. Test items were chosen so that the following five areas were represented: number sense, geometric/spatial sense, patterns and relationships, mathematical systems and number theory, and discrete mathematics.

Procedures

The primary objective of this study was to ascertain the effect that the read-aloud accommodation had on the validity of math test scores and reading comprehension test scores. It is usually assumed that achievement tests (e.g., a math test) measure a single ability, and the ability that is measured is the same in each sub-population. When a test measures a different ability in two sub-populations, score interpretation becomes very difficult. It does not mean that the test is valid in one population but not in the other, only that the meaning of the scores is different across populations. This difference makes it difficult to discuss the effects of various conditions on test score validity. The resolution is to select one group as the standard against which the interpretation of the validity of scores for other groups is described. This standard group is called the reference group.

Many methods have been developed to ascertain whether a test measures the same trait in two groups. The method chosen in this study uses item response theory. Item response theory constitutes a set of mathematical models and assumptions that define the probability of getting an item correct as a function of an examinee’s ability and item characteristics. When the assumptions hold and the model fits the data, the item characteristics are not dependent on the characteristics of a particular population. One such item characteristic is item difficulty.

It has been argued that an item difficulty difference of sufficient magnitude indicates that the item is measuring a different ability for the two groups. These items are referred to as DIF (differential item functioning) items. The presence of many DIF items suggests that the test measures different abilities for different groups of examinees. This study compared the item difficulty estimates from each of the four groups defined above. The question to be answered was whether item difficulty estimates generated using a unidimensional three-parameter logistic model were substantially different for students receiving the read-aloud accommodation compared to students who took the test without an accommodation.

Accommodations research using extant data is complicated by the fact that the use of test accommodations is confounded by the presence of a disability and low achievement. Students without a disability usually do not receive accommodations and score well-above students with disabilities. Thus, students receiving accommodations typically differ from non-accommodated students in three ways: (1) lower performance, (2) the presence of a disability, and (3) the presence of an accommodation. Identifying four groups of examinees allows us to begin to isolate the effect of the read-aloud accommodation. First, a random sample of students without disabilities who do not use accommodations was selected to serve as the reference group (Group A). The item structure for this group serves as the standard for what the test was designed to measure. A random sample of low ability students without disabilities was used to study the effect for the overall performance difference (Group B). A group of students with an IEP in reading who took the test under standard conditions was used to study the effect that the disability has on the construct being measured (Group C). Item difficulty differences between Group C and Group A represent the effect of the disability plus the effect for the overall performance difference; therefore, the effect found for the former group must be subtracted from the effect for this group in order to study the effect for the disability. Last, a group of students with an IEP in reading who received the read-aloud accommodation (Group D) was used to study the effect that the accommodation had on the construct being measured. Item difficulty differences between Group D and Group A include any effect of the accommodation plus the effect of the disability plus the effect of the overall performance difference; therefore, the effect attributed to Group C must be subtracted from the effect for Group D in order to study the effect for the accommodation.

The program, BILOG-MG, was used to fit the three-parameter logistic model to the data (Zimkowski, Muraki, Mislevy, & Bock, 1996). BILOG-MG makes it possible to produce item difficulty estimates on several groups simultaneously; all that is required is to define one group as the reference group and the other groups as focal groups. The reference group is used to set the location (mean) and the metric (standard deviation) of the item difficulty scale. Item difficulty estimates for each focal group are placed onto the scale of the reference group by applying two sets of constraints. First, BILOG-MG constrains the item discrimination and pseudo-guessing parameters to be equal across groups for each item. Second, it constrains the sum of the item difficulty estimates in the focal groups to equal the sum of the item difficulty estimates in the reference group. After applying these constraints, the resulting item difficulty estimates are on a common scale and mathematical operations can be applied to them.

The effect that the overall performance difference, the presence of the disability, and the use of the read-aloud accommodation had on item difficulty can be ascertained by comparing the item difficulty difference between conditions (focal group item difficulty minus reference group item difficulty). Because the difference may be either negative or positive, it is necessary to square the difference so that the sum will produce a positive number that indicates the overall magnitude across all test items. The square root of the average squared discrepancy is referred to as the root-mean-squared discrepancy (RMSD). The formula for the RMSD is shown here:

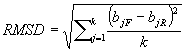
where j represents the jth item, k is the number of items on the test, bjF is the logit item difficulty estimate on the jth item for the focal group and bjR is the logit item difficulty estimate on the jth item for the reference group. The RMSD gives a measure of the overall item difficulty difference across all test items. A large RMSD suggests that the items operated differently in the focal group compared to the reference group.

The magnitude of the RMSD is a function of the effect of interest as well as measurement and sampling error. One would expect the RMSD to be some value greater than zero even between two randomly equivalent groups. An estimate of the amount of the RMSD that could be attributed to estimation error was ascertained by computing the RMSD between two random samples of approximately 1000 general education students. This value is analogous to the error term in the denominator of a t-test. A judgment of statistical significance could be made by computing the ratio of the RMSD from one of the focal groups to the RMSD that results from estimation error.

Another way to ascertain the magnitude of each effect would be to compare the fit of the 3-parameter logistic (PL) model when the item difficulties are constrained to be equal across groups versus the model in which item difficulties are allowed to vary across groups. BILOG-MG calculates the –2 log likelihood statistic, which can be used to judge the goodness of fit of the model to the data. In order to ascertain the magnitude of each effect, one analysis was conducted in which the item difficulty estimates for the reference group (Group A) and each focal group (Group B, C, and D) were constrained to be equal across groups. A second analysis was conducted using the DIF option in BILOG-MG. The DIF option allows the item difficulties to vary across groups. The difference in the –2 log likelihood statistic between the two analyses provides an indication of the overall magnitude of the effect. Twelve analyses were conducted, two for each effect on both the reading and math test items.

BILOG-MG computes the item difficulty difference across groups (bjF - bjR) after the items have been rescaled to a common scale, and it generates the standard error of this difference. The standard error can be used to determine whether the difference statistically differs from zero (no difference). Items for which the ratio of the difficulty difference to the standard error exceeds 2.0 indicate that the item is measuring something different in the two groups, which is known as differential item functioning, or DIF for short. The number of DIF items was also used to ascertain the magnitude of the effect of each condition; the presence of many DIF items is compelling evidence that a test functions differently for two groups.

Average Squared Discrepancy Results

Reading Test

The effect of the read-aloud accommodation on item difficulty was described in three ways. First, discrepancies between the item difficulty estimates for Group A and each of the focal groups (Groups B, C, and D) were computed. Table 2 summarizes the results from the reading test. The table reports the median squared discrepancy and not the mean squared discrepancy because the distribution of the item difficulty differences was positively skewed. The median squared discrepancy between the low performing general education students (Group B) and the random sample of general education students (Group A) was only .009, thus indicating that the rescaled item difficulty estimates were very similar for these groups. Because these values are squared, it is necessary to take the square root to obtain the magnitude of the discrepancy; therefore, the median squared discrepancy for Group B corresponds to an average item difficulty difference between Group B and Group A of about .10 (i.e., the square root of .009). The median squared discrepancy for the group of students with an IEP in reading taking the reading test without an accommodation (Group C) was .042, or four times greater than the median squared discrepancy between Group B and Group A. The students with an IEP in reading who took the reading test with the read-aloud accommodation (Group D) had a median squared discrepancy of .086, which was 10 times greater than the median squared discrepancy between Group B and Group A.

Table 2. The Average Squared Discrepancy Between the Item Difficulty Estimates Obtained on the Focal Groups (Groups B, C, and D) and the Reference Group (Group A) on the Reading Test

  Squared Discrepancy
Effect Median Maximum 75th Percentile
Performance alone1 .009 .099 .021
Perf. + Disability2 .042 1.724 .091
Perf. + Dsbl. + Accommodation3 .086 4.792 .310

1Perf = Group B compared to Group A
2Perf + Disability = Group C compared to Group A
3Perf + Dsbl + Accommodation = Group D compared to Group A

The distribution of squared discrepancies was skewed, as evidenced by the magnitude of the maximum value compared to the value at the 75th percentile. For Group C the value of squared discrepancy corresponding to the 75th percentile was .091 on the reading test, whereas the maximum value was 1.72. In other words, the largest squared discrepancy (1.72) was 19 times larger than the squared discrepancy corresponding to the 75th percentile. In Group D, the maximum squared discrepancy was 4.79, which was more than 15 times larger than the squared discrepancy corresponding to the 75th percentile. A cursory examination of Appendix A indicates that the last three questions on the reading test were much more difficult for the students with an IEP in reading (groups C and D) than for the general education students. It is important to note that these differences are not the result of overall performance because the rescaling controls for overall performance differences. It is not clear why the last three items were so much harder for the students with an IEP in reading. An examination of frequency of not attempting each item indicates that this alone cannot account for the large difficulty difference. About 1% of the students in Groups A, B, and C did not attempt these items, compared to over 2% of the students in Group D. Removing the last three items from the results would dramatically reduce the amount of skew in the distribution of squared discrepancies.

 

Math Test

Table 3 contains the summary of the squared discrepancies between the item difficulty estimates for each of the focal groups (Groups B, C, and D) and the reference group (Group A). The median squared discrepancy for Group B was quite small (.008), which is about the same magnitude as the median squared discrepancy for Group B on the reading test. A value this small indicates that the rescaled item difficulty estimates were similar between Group B and Group A. Unlike the results on the reading test, the median squared discrepancies for Group C and Group D were relatively small, .023 and .022 respectively. A squared discrepancy of this magnitude indicates that, on average, the item difficulty difference between the reference group and each of the focal groups was in the order of .10 to .20. The distribution of squared discrepancies was not as skewed on the math test as it was on the reading test, thus indicating that no item or subset of items would dramatically influence the results (see Appendix B).

Table 3.The Average Squared Discrepancy Between the Item Difficulty Estimates Obtained on the Focal Groups (Groups B, C, and D) and the Reference Group (Group A) on the Math Test

  Squared Discrepancy
Effect Median Maximum 75th Percentile
Performance alone1 .008 .425 .039
Perf. + Disability2 .022 .521 .124
Perf. + Dsbl. + Accommodation3 .023 .286 .071

1Perf = Group B compared to Group A
2Perf + Disability = Group C compared to Group A
3Perf + Dsbl + Accommodation = Group D compared to Group A

Fit Results

Two fit indices were used to estimate the magnitude of each effect—the effect due to the performance difference, the effect due to the disability, and the effect due to the read-aloud accommodation. One index, called the root mean squared discrepancy, gauges the overall discrepancy between item difficulty estimates between the reference group and each focal group. When the model fits the data and there is no estimation error, the RMSD should equal zero. However, a portion of the variance in these item difficulty differences can be attributed to the estimation error. The magnitude of the estimation error is a function of both the number and quality of the items, and the number of examinees. In order to estimate how much of the RMSD can be attributed to estimation error, the RMSD between two random samples of general education students each with about 1000 students was computed. The RMSD between these two samples provides an estimate of the amount of estimation error present in the other comparisons.

The –2 log likelihood difference between the unconstrained and the constrained model was also used to evaluate each effect. For the unconstrained model, item difficulty was allowed to vary between the reference group and the focal group. For the constrained model, the item difficulty estimates were constrained to be equal across groups. A large –2 log likelihood indicates that the item difficulties are not the same between the focal group and the reference group.

Table 4 displays the RMSD and the –2 log likelihood fit index (G2c – G2u) for each focal group/reference group comparison. The effects present in each comparison are shown in the left column. Each effect was isolated by subtracting the RMSD of the comparison that contains all of the effects except for the effect to be isolated. For instance, the effect due to the learning disability was calculated by subtracting the RMSD due to performance from the RMSD due to performance and disability. The statistical significance of this effect was determined by calculating the ratio of that difference to the RMSD attributable to estimation error. The ratio follows a t-distribution; therefore, an absolute value greater than 2.0 indicates a statistically significant effect. For a one-tailed hypothesis test with 40 degrees of freedom on the reading test, the critical t is 1.684, and for the 31 degrees of freedom on the math test the critical t is 1.696.

 

Table 4. The RMSD Between the Reference Group and the Focal Group, and the –2 Log Likelihood Fit Between the Constrained (G2c) and the Unconstrained Model (G2u)

  Reading Math
Effect RMSD G2C-G2U RMSD G2C-G2U
Estimation error .11   .19  
Performance alone .131 7122 .20 614
Perf + Disability .361 8432 .22 605
Perf + Disability + Accommodation .671 12612 .30 612

 

Reading Test

For the reading test, the effect due to estimation error resulted in an RMSD of .11. The effect due to the overall performance difference was .13, which is about the same magnitude as that due to estimation error, indicating that the effect was not significant. The RMSD was roughly three times larger (RMSD = .36) when the presence of the disability was added, and it was roughly six times larger (RMSD = .67) when the effect for the disability plus the effect for the accommodation was included. The effect for reading disability was .23 (.36 - .13) and it was significant (t = 2.09). The effect due to the read-aloud accommodation was .31 (.67 - .36), which is also significant (t = 2.82).

The –2 log likelihood difference between the constrained and unconstrained model for each effect displayed a similar pattern of increasing magnitude. When the two groups (reference and focal) differ only on ability, the difference in the –2 log likelihood was 712, it increased to 843 with the addition of the effect for disability, then jumped to 1261 with the addition of the effect for the read-aloud accommodation. The difference between the –2 log likelihood is distributed as a chi-square. The degrees of freedom for the chi-square test is equal to the number of items on the test. Each of the effects resulted in significantly poorer model fit. In other words, the item difficulties are not the same across groups.

The last three items on the reading test had much larger item difficulty differences (Reference Group – Focal Group) than the other items. The item difficulty difference was -.83, -1.02, and –1.31 in the comparison between Group C and Group A, and it was –2.04, -1.91, and –2.19 in the comparison between Group D and Group A. In other words, these items were much harder for the two reading disability groups. The RMSD was recalculated without the last three items, with a result of a RMSD of .22 for Group C and .40 for Group D. The effect due to the presence of the reading disability was recalculated: t = [(.22-.13)/.11] = .82.

After removing the last three items, the effect for reading disability was no longer significant. The effect due to the read-aloud accommodation was also recalculated and was not significant (t = [(.40-.22)/.11] = 1.64), although it was close to the critical value of 1.68.

 

Math Test

Each of the effects was negligible on the math test. The magnitude of estimation error was .19. The RMSD for the effect due to the overall performance difference was .20. As with the reading test, the effect for the overall performance difference was not statistically significant. The presence of the performance difference plus the reading disability resulted in a RMSD equal to .22, and a t equal to .10. The result indicates that the presence of a reading disability does not significantly change the construct being measured. In the absence of a significant effect for the reading disability, it makes little sense to determine whether the use of the read-aloud accommodation significantly reduces the item difficulty discrepancies. However, the effect was computed to determine whether the presence of the read-aloud accommodation made matters worse. The t associated with the combined effect of the reading disability and the read-aloud accommodation was .53, not statistically significant. The magnitude of the difference in model fit ranged from 605 for Group C to 614 for Group B. The fit statistic suggests that neither disability status nor accommodation status, nor the combination of the two, had an overall DIF effect.

DIF Item Results

The third way in which the effect of each condition (i.e., the effect for ability differences, the effect for disability status, and the effect for the accommodation) was examined was to count the number of DIF items for each group. An item was considered a DIF item if the ratio of the item difficulty difference ([bf –br]/SE(bf-br)) exceeded 2.0. Because this ratio is distributed as a t-distribution, a value of 2.0 indicates statistical significance for a two-tailed alpha equal to .05. Table 5 shows the number of DIF items for each group on each test. Only one item was flagged as DIF for Group B on the reading test, and none were flagged on the math test. Group C had 10 DIF items on the reading test, and only one DIF item on the math test. Finally, Group D had 19 DIF items on the reading test and six DIF items on the math test.

Table 5. The number of DIF items

Number of DIF items

Group

Reading

Math

B

 1

0

C

10

1

D

19

6


Discussion

The goal of this study was to ascertain whether the read-aloud accommodation altered the construct being measured by a reading test and a math test. Specifically, it was argued that item characteristics for students with a reading disability taking a math test and a reading test with the read-aloud accommodation should be the same as those for students without disabilities taking each test without the accommodation, whereas the item characteristics for students with a reading disability taking each test without the read-aloud accommodation should differ from the reference group.

Because the students receiving the accommodation differed from the reference group on three conditions—ability level, disability status, and use of an accommodation—a direct comparison between the reference group and the group receiving the read-aloud accommodation would be confounded. It was necessary to include two additional comparison groups—one that estimates the effect of the ability difference, and one that estimates the effect of the combination of the ability and disability status. Although we did not have the advantage of random assignment to all conditions, by using three focal groups, the effect of the read-aloud accommodation could be estimated.

The root-mean-squared-discrepancy was used to index the overall item discrepancy. A large RMSD suggests that the test items measure different constructs. The extent to which the test items measured the same construct for the three conditions was also evaluated by a count of the number of items that differed significantly from the estimate in the non-disabled, non-accommodated sample. These were called DIF items.

 

Reading Test

The results from the reading test indicated that item difficulty was substantially different from the reference group for students with a reading disability taking the test without an accommodation. In other words, in the absence of an accommodation, reading comprehension test scores will not mean the same thing for students with a reading disability as they do for other examinees. This type of evidence suggests that some alteration to the regular test is necessary to obtain comparable scores for students with and without a reading disability.

Providing certain accommodations to students with a reading disability is one way to obtain comparable scores. A common accommodation is to read the test passages and items to the students. The results of this study do not support this approach. When the read-aloud accommodation was provided to students with a reading disability, the item difficulty differences actually increased. The RMSD was two times greater for the students receiving the read-aloud accommodation than for students taking the test without it. Furthermore, the number of DIF items nearly doubled from 10 items for the students taking the test without the accommodation to 19 items for students taking the test with the read-aloud accommodation.

Reading the reading test made a bad situation worse. Because students were not randomly assigned to conditions, these results cannot be used to declare that reading the reading test represents an invalid accommodation. However, this demonstrates that the score for students receiving this accommodation in an actual testing situation results in scores that do not mean the same thing as the scores for the students without disabilities who do not receive accommodations.

Item difficulty differences on the reading test were most pronounced on the last three items. The item difficulty difference exceeded one standard deviation unit on each of these three items. The direction of the difference indicated that these items were much more difficult for the students with a reading disability, whether they had the accommodation or not. When these items were removed, and the RMSD was recomputed, the overall difference between the item difficulty estimates for students with a reading disability taking the test without an accommodation and the non-disabled reference group were no longer statistically significant. Removing these items resulted in a non-statistically significant effect for the reading disability. This implies that, after removing the last three items, the overall test scores for students with a reading disability taking the test without an accommodation measure the same latent trait as test scores for the non-disabled, non-accommodated group. This was not the result for the students receiving the read-aloud accommodation. Even with the last three items removed, the RMSD still indicated that test scores were not a measure of the same latent trait as they were for students in the reference group. The presence of the read-aloud accommodation made things worse.

 

Math Test

Item difficulty estimates for students with a reading disability taking the math test without an accommodation did not differ significantly from the item difficulty estimates for the reference group. In all, only one item was identified as a DIF item. Overall, the item difficulty estimates were not significantly different from the reference group when students with a reading disability took the math test using the read-aloud accommodation. These results suggest that test scores for the students with a reading disability measured the same trait as they did in the reference group, regardless of whether the student with a disability received the accommodation. However, 6 of the 31 items were identified as DIF items. This finding indicates that the read-aloud accommodation altered the characteristics of some of the items. Four of the six items were statistically easier for the students receiving the accommodation than for the reference group after controlling for the overall performance difference. If these items were word problems, it might suggest that the accommodation removed extraneous difficulty due to the reading load of the item. This study cannot verify this, but does point to the need to attach DIF results to item characteristics.

The results from the math test provide a mixed picture. On the one hand, the findings indicate that the use of the read-aloud accommodation did not significantly alter item difficulty estimates. However, not reading the math test to students with a reading disability did not result in poor measurement either. Since the items seem to function the same for students with a reading disability without an accommodation as they do for general education students, one might wonder what the point would be in providing the read-aloud accommodation. Without the accommodation, only one item was flagged as DIF; with the accommodation, six items were flagged as DIF. It appears that providing the read-aloud accommodation to students with a reading disability makes a good situation bad.

One possible explanation for why the read-aloud accommodation resulted in more DIF items is that administration of the read-aloud accommodation may have been flawed. Also, it may be that the read-aloud accommodation was not uniformly administered across schools. Non-uniform administration would introduce additional random error to the test score, which could result in less stable item difficulty estimates. One can easily imagine ways in which the read-aloud accommodation could differ from test proctor to test proctor. For instance, one proctor may read with more pronounced voice inflexions and examinees could construe them to represent a clue to the answer. This could also detract the examinee from solving the problem by herself or himself, and instead focus on unreliable cues. Other distractions may pose more of a problem when a proctor reads test material than when a student reads it. If one becomes distracted while reading, one could reread the material preceding the distraction. However, one does not have this luxury when a proctor reads the material. Presentation of the read-aloud via recording with a well-trained reader may mitigate these problems.

Another potential problem can be attributed to group presentation of the read-aloud accommodation. In Missouri, the read-aloud is administered by having a proctor read the item and response choices to a small group of students or to individual students. A student may ask the proctor to re-read the problem. However, social pressures may limit these requests even if the students or group of students did not attend well to the initial reading. Because listening is a more passive activity than reading, it is easy to imagine that a student may not be attending well to the proctor, catching a student “off-guard” will likely result in that student missing the item. Furthermore, it is likely that students are aware of the behavior of other students in the room. When the correct answer is read, a student may watch how the other students react to each response option, and then make their choice when the other students seem to be marking their choice.

There also is the possibility that the read-aloud accommodation was not given to the students who actually needed it and was given to students who did not need it. This possibility seems unlikely given that the analysis only included students with a reading disability, however we have no basis for knowing whether some students with a reading disability might need an accommodation while others with the same disability might not. Presumably students with a reading disability should benefit from the accommodation, whereas students without a reading disability should not. It is possible that the identification of students with a reading disability is inadequate.

There is also the possibility that the read-aloud accommodation is itself flawed, or that it is simply unnecessary for the vast majority of students with reading disabilities. Our findings indicate that the effect for the reading disability was not significant on the math test; additionally, only one DIF item was identified. These results indicate that the construct of the math test was not affected by the presence of the disability; thus, there was no reason to accommodate those students. Similarly, after removing the last three items on the reading test, the effect due to the reading disability was not significant. That is, reading comprehension test items tapped the same construct for students with a reading disability as they did for the students without the reading disability.

Our findings indicate that either the read-aloud accommodation was unnecessary for students with reading disabilities taking a 3rd grade reading comprehension test and a 4th grade math test, or that only a subgroup of these students would benefit from the accommodation. This study is just a first step in establishing the effect of the read-aloud accommodation on the construct validity of a reading and math test. Strong conclusions about the validity of the read-aloud accommodation itself will require the accumulation of evidence from many studies, including more analysis of extant data.

References

Anastasi, A. (1988). Psychological testing (6th Ed). New York, NY: Macmillan Publishing Company.

Bielinski, J., Ysseldyke, J., Bolt, S., Friedebach, M., & Friedebach, J. (in press). Prevalence of accommodations for students with disabilities participating in a statewide testing program. Diagnostique.

Elliott, S. N., Kratochwill, T. R., McKevitt, B, Schulte, A. G., Marquart, A. & Mroch, A. (June, 1999). Experimental analysis of the effects of testing accommodations on the scores of students with and without disabilities: Mid-project results. A paper presented at the CCSSO Large-Scale Assessment Conference, Snowbird, Utah, June, 1999.

Fuchs, L. S., Fuchs, D., Eaton, S. B., Hamlett, C., & Karns, K. (2000). Supplementing teacher judgments about test accommodations with objective data sources. School Psychology Review, 29 (1), 65-85.

Fuchs, L. S., Fuchs, D., Eaton, S. B., Hamlett, C., Binkley, E., & Crouch, R. (Fall, 2000). Using objective data sources to enhance teacher judgments about test accommodations. Exceptional Children 67 (1), 67-81.

Phillips, S. E. (1994). High stakes testing accommodations: Validity vs. disabled rights. Applied Measurement in Education, 7 (2), 93-120.

Pomplun, M., & Omar, H. M. (2000). Score comparability on a state mathematics assessment across students with and without reading accommodations. Journal of Applied Psychology, 85 (1), 21-29.

Thurlow, M., House, A., Boys, C., Scott, D., & Ysseldyke, J. (2000). State participation and accommodation policy for students with disabilities: 1999 update (Synthesis Report 33). Minneapolis, MN: National Center on Educational Outcomes.

Thurlow, M., & Weiner, D. (2000). Non-approved accommodations: Recommendations for use and reporting (Policy Directions No. 11). Minneapolis, MN: University of Minnesota, National Center on Educational Outcomes

Tindal, G., Heath, B., Hollenbeck, K., Almond, P., & Harniss, M. (1998). Accommodating students with disabilities on large-scale tests: An experimental study. Exceptional Children, 64(4), 439-451.

Tindal, G., Helwig, R., & Hollenbeck, K. (1999). An update on test accommodations: Perspectives of practice to policy. Journal of Special Education Leadership, 12(2), 11-20.

Tippets, E., & Michaels, H.(1997). Factor structure invariance of accommodated and non-accommodated performance assessments. Paper presented at the National Council on Measurement in Education annual meeting, Chicago.

Willingham, W. (1988). Testing handicapped people: The validity issue. In Wainer, & Braun, (Ed). Hillsdale: NJ: Lawrence Erlbaum.

Appendix A

Reading Test Adjusted Threshold Values

 

   ITEM                    GROUP

                  A          C          D          B         

 

   R01      |  -3.574  |  -3.971   |  -4.155  |  -3.649 

            |   0.272* |    0.228* |   0.249* |   0.207*

   R02      |  -3.220  |  -3.429   |  -3.082  |  -3.312 

            |   0.223* |    0.166* |   0.172* |   0.149*

   R03      |  -0.614  |  -0.715   |  -0.646  |  -0.608 

            |   0.128* |    0.140* |   0.130* |   0.120*

   R04      |  -1.843  |  -2.132   |  -2.427  |  -1.818 

            |   0.302* |    0.288* |   0.293* |   0.268*

   R05      |  -1.511  |  -1.421   |  -1.085  |  -1.666 

            |   0.126* |    0.110* |   0.095* |   0.098*

   R06      |  -1.606  |  -1.913   |  -1.991  |  -1.647 

            |   0.155* |    0.155* |   0.146* |   0.129*

   R07      |  -1.378  |  -1.552   |  -1.504  |  -1.569 

            |   0.138* |    0.130* |   0.121* |   0.116*

   R08      |  -1.667  |  -1.636   |  -1.881  |  -1.850 

            |   0.119* |    0.111* |   0.111* |   0.102*

   R09      |  -0.582  |  -0.476   |  -0.646  |  -0.654 

            |   0.077* |    0.089* |   0.079* |   0.069*

   R10      |  -3.005  |  -3.305   |  -3.278  |  -3.104 

            |   0.220* |    0.181* |   0.192* |   0.164*

   R11      |   0.194  |  -0.158   |  -0.811  |   0.189 

            |   0.092* |    0.130* |   0.111* |   0.115*

   R12      |   0.106  |  -0.098   |  -0.506  |  -0.001 

            |   0.046* |    0.076* |   0.057* |   0.061*

   R13      |  -0.799  |  -0.549   |  -0.571  |  -0.536 

            |   0.130* |    0.137* |   0.124* |   0.113*

   R14      |   0.758  |   0.591   |   0.681  |   0.652 

            |   0.063* |    0.154* |   0.140* |   0.111*

   R15      |  -0.990  |  -1.017   |  -1.267  |  -0.994 

            |   0.093* |    0.091* |   0.086* |   0.077*

   R16      |  -1.244  |  -1.203   |  -1.261  |  -1.153 

            |   0.093* |    0.086* |   0.078* |   0.072*

   R17      |   0.020  |  -0.072   |  -0.212  |   0.334 

            |   0.121* |    0.162* |   0.140* |   0.147*

   R18      |  -1.344  |  -1.058   |  -0.975  |  -1.235 

            |   0.127* |    0.112* |   0.104* |   0.100*

   R19      |   0.421  |   0.441   |   1.036  |   0.564 

            |   0.049* |    0.141* |   0.218* |   0.105*

   R20      |  -1.729  |  -1.994   |  -1.785  |  -1.843 

            |   0.133* |    0.124* |   0.116* |   0.107*

   R21      |   0.278  |  -0.116   |  -0.538  |   0.422 

            |   0.055* |    0.086* |   0.069* |   0.089*

   R22      |  -0.052  |  -0.378   |  -0.270  |  -0.119 

            |   0.058* |    0.080* |   0.075* |   0.073*

   R23      |  -0.111  |  -0.172   |  -0.413  |  -0.397 

            |   0.085* |    0.119* |   0.101* |   0.090*

   R24      |  -0.727  |  -1.062   |  -1.465  |  -0.816 

            |   0.079* |    0.084* |   0.085* |   0.069*

   R25      |   0.073  |   0.411   |   0.366  |   0.290 

            |   0.088* |    0.164* |   0.143* |   0.117*

   R26      |  -0.292  |  -0.418   |  -0.784  |  -0.132 

            |   0.089* |    0.109* |   0.096* |   0.095*

   R27      |  -0.348  |  -0.491   |  -0.501  |  -0.315 

            |   0.067* |    0.082* |   0.077* |   0.069*

   R28      |  -0.698  |  -0.969   |  -0.980  |  -0.604 

            |   0.100* |    0.108* |   0.102* |   0.092*

   R29      |  -1.479  |  -1.490   |  -1.361  |  -1.431 

            |   0.125* |    0.112* |   0.103* |   0.097*

   R30      |  -0.596  |  -0.714   |  -0.928  |  -0.673 

            |   0.112* |    0.121* |   0.111* |   0.101*

   R31      |  -0.659  |  -0.865   |  -1.060  |  -0.797 

            |   0.068* |    0.073* |   0.070* |   0.061*

   R32      |  -0.932  |  -0.856   |  -1.263  |  -0.958 

            |   0.083* |    0.079* |   0.077* |   0.068*

   R33      |  -0.484  |  -0.738   |  -0.943  |  -0.467 

            |   0.086* |    0.096* |   0.091* |   0.082*

   R34      |   0.407  |   0.531   |   0.333  |   0.700 

            |   0.063* |    0.151* |   0.109* |   0.120*

   R35      |  -0.848  |  -0.565   |  -0.832  |  -0.703 

            |   0.087* |    0.090* |   0.080* |   0.073*

   R36      |  -2.020  |  -1.833   |  -1.950  |  -2.115 

            |   0.286* |    0.258* |   0.257* |   0.245*

   R37      |  -0.575  |  -0.578   |  -0.027  |  -0.492 

            |   0.150* |    0.158* |   0.160* |   0.134*

   R38      |  -0.129  |   0.012   |   0.044  |  -0.270 

            |   0.087* |    0.135* |   0.118* |   0.094*

   R39      |   0.160  |   0.985   |   2.199  |   0.054 

            |   0.096* |    0.245* |   0.510* |   0.119*

   R40      |  -2.051  |  -1.030   |  -0.137  |  -1.959 

            |   0.187* |    0.140* |   0.144* |   0.135*

   R41      |  -1.348  |  -0.035   |   0.841  |  -1.355 

            |   0.182* |    0.187* |   0.241* |   0.146*

 --------------------------------------

 *STANDARD ERROR

 

Appendix B

Math Test Adjusted Threshold Values

 

   ITEM                         GROUP

                  A          C          D          B        

 

   M01      |  -4.411  |  -4.030   |  -3.764  |  -3.996 

            |   0.504* |    0.418* |   0.413* |   0.415*

   M02      |  -2.524  |  -2.378   |  -2.006  |  -2.533 

            |   0.323* |    0.280* |   0.267* |   0.283*

   M03      |  -0.166  |   0.095   |   0.553  |  -0.167 

            |   0.173* |    0.200* |   0.201* |   0.178*

   M04      |  -3.904  |  -4.203   |  -4.172  |  -4.561 

            |   0.377* |    0.328* |   0.332* |   0.339*

   M05      |  -3.396  |  -3.998   |  -3.898  |  -3.631 

            |   0.586* |   0.570*  |   0.566* |    0.554*

   M06      |  -1.179  |  -1.105   |  -1.151  |  -1.113 

            |   0.131* |    0.124* |   0.111* |   0.118*

   M07      |  -0.852  |  -0.762   |  -0.653  |  -0.866 

            |   0.073* |    0.073* |   0.063* |   0.068*

   M08      |  -1.691  |  -1.572   |  -1.442  |  -1.866 

            |   0.177* |    0.160* |   0.144* |   0.162*

   M09      |  -0.611  |  -0.816   |  -1.029  |  -0.671 

            |   0.101* |    0.108* |   0.094* |   0.102*

   M10      |   0.021  |  -0.053   |   0.044  |   0.058 

            |   0.093* |    0.118* |   0.105* |   0.109*

   M11      |   0.383  |   0.313   |   0.502  |   0.420 

            |   0.088* |    0.134* |   0.123* |   0.125*

   M12      |  -1.431  |  -0.975   |  -0.924  |  -1.156 

            |   0.122* |    0.105* |   0.094* |   0.100*

   M13      |  -2.401  |  -2.718   |  -2.550  |  -2.771 

            |   0.228* |    0.211* |   0.205* |   0.211*

   M14      |  -2.710  |  -2.336   |  -2.628  |  -2.660 

            |   0.201* |   0.160*  |   0.165* |    0.163*

   M15      |  -1.569  |  -1.732   |  -1.866  |  -1.864 

            |   0.143* |    0.134* |   0.128* |   0.129*

   M16      |  -2.615  |  -2.440   |  -2.667  |  -2.785 

            |   0.180* |    0.158* |   0.162* |   0.163*

   M17      |  -1.911  |  -1.858   |  -1.856  |  -1.962 

            |   0.166* |    0.150* |   0.141* |   0.146*

   M18      |  -1.492  |  -1.623   |  -1.590  |  -1.401 

            |   0.218* |    0.205* |   0.194* |   0.196*

   M19      |  -1.201  |  -1.260   |  -1.455  |  -1.050 

            |   0.106* |    0.100* |   0.094* |   0.094*

   M20      |  -1.527  |  -1.506   |  -1.471  |  -1.532 

            |   0.120* |    0.108* |   0.096* |   0.101*

   M21      |  -0.052  |  -0.101   |  -0.237  |  -0.072 

            |   0.077* |    0.100* |   0.081* |   0.091*

   M22      |  -0.542  |  -0.834   |  -0.967  |  -0.733 

            |   0.124* |    0.130* |   0.118* |   0.125*

   M23      |  -0.255  |  -0.240   |  -0.131  |  -0.256 

            |   0.088* |    0.104* |   0.092* |   0.096*

   M24      |   0.122  |  -0.086   |  -0.139  |   0.211 

            |   0.049* |    0.068* |   0.056* |   0.069*

   M25      |   0.006  |  -0.188   |  -0.125  |   0.199 

            |   0.066* |    0.084* |   0.073* |   0.087*

   M26      |  -1.235  |  -1.087   |  -1.163  |  -1.218 

            |   0.092* |    0.084* |   0.074* |   0.079*

   M27      |  -0.470  |  -0.566   |  -0.604  |  -0.364 

            |   0.065* |    0.073* |   0.061* |   0.072*

   M28      |  -1.287  |  -1.123   |  -1.407  |  -1.243 

            |   0.131* |    0.117* |   0.109* |   0.112*

   M29      |   0.466  |   0.491   |   0.597  |   0.765 

            |   0.057* |    0.115* |   0.105* |   0.119*

   M30      |  -0.755  |  -0.772   |  -0.885  |  -0.546 

            |   0.075* |    0.078* |   0.067* |   0.075*

   M31      |  -1.143  |  -0.914   |  -0.885  |  -0.971 

            |   0.163* |   0.154*  |   0.139* |   0.148*

   M32      |   0.230  |   0.276   |  -0.133  |   0.237 

            |   0.106* |    0.145* |   0.112* |   0.132*

-------------------------------

 *STANDARD ERROR

Top of page