Effect of Minimum Cell Sizes and Confidence Interval Sizes for Special Education Subgroups on School-Level AYP Determinations
NCEO Synthesis Report 61
Published by the National Center on Educational Outcomes
Mary Ann Simpson • Brian Gong • Scott Marion
The National Center for the Improvement of Educational Assessment
July 2006
Any or all portions of this document may be reproduced and distributed without prior permission, provided the source is cited as:
Simpson, M. A., Gong, B., & Marion, S. (2006). Effect of minimum cell sizes and confidence interval sizes for special education subgroups on school-level AYP determinations (Synthesis Report 61). Minneapolis, MN: University of Minnesota, National Center on Educational Outcomes. Retrieved [today's date], from the World Wide Web: http://cehd.umn.edu/NCEO/OnlinePubs/Synthesis61.html
Executive Summary
This study addresses three questions:
First, considering the full group of students and the special education subgroup, what is the likely effect of minimum cell size and confidence interval size on school-level AYP determinations?
Second, what effects do the changing minimum cell sizes have on inclusion of special education students, especially for schools that are declared as "meeting AYP"?
Third, with the NCLB requirement that schools assess grade levels 3–8 in their AYP calculations beginning in the 2005–2006 academic year, what is the likely effect of including these additional students in school-level AYP determinations?
To address these questions, data from five states were used to model confidence interval and cell-size combinations. The study used a single year of elementary/middle school mathematics and reading achievement test data from five states, modeling selected minimum cell sizes from 10 to 100, and confidence interval sizes from 70% to 99%.
Increases in minimum cell sizes for the special education subgroup were associated with a large increase in the number of schools meeting AYP targets for each of the five states assessed. Increased confidence interval sizes were also associated with an increase in pass rates, but a much smaller increase. While raising the minimum-n is an effective means of increasing the passing rates of schools, it does so at a considerable cost to special education students in terms of being excluded from the accountability system. When the data were modeled to reflect testing in all grades 3–8, many more special education students’ results are included in the accountability system, assuming that states will not increase the minimum-n. If the implicit theory of action guiding NCLB accountability requirements is to improve instruction and thus outcomes for all students, schools and districts must be accountable for all subgroups in order to ensure that these students are appropriately served. The effect of increasing the minimum-n to exclude substantial portions of special education students must be considered a threat to the validity of the accountability system.
Judging School Performance under NCLB
The "No Child Left Behind Act" (NCLB) requires that schools be held accountable for the performance of the school as a whole as well as for designated subgroups, beginning with the 2002–2003 academic year. Subgroups specified by NCLB include racial/ethnic groups, economically disadvantaged students, students with disabilities, and students with limited English proficiency. States are required to determine whether, for each school, the school as a whole and each subgroup within the school has met a set of Annual Measurable Objectives (AMOs) in reading/English language arts and mathematics. In general, the AMOs are the percent of students who score proficient or above on the state assessments. NCLB also requires that a judgment be made annually whether every school did or did not "make AYP." AYP stands for "Adequate Yearly Progress," which is a term inherited from previous versions of the legislation. In fact, under NCLB schools do not have to make any progress from year to year as long as they are above the AMO. If the state AMO is 45% in reading, to meet Adequate Yearly Progress (AYP) a school would need to have at least 45% of all its eligible students score proficient or above, and also have at least 45% of the students in each subgroup score proficient or above: at least 45% of the students with disabilities, 45% of the African-American students, and 45% of its Native American students, and so on. If one group fails to meet the AMO, then the school does not meet AYP. A school that fails to meet AYP two or more years faces specific sanctions established by NCLB and/or the state. The AMOs under NCLB rise over time until the requirement is 100% of students scoring proficient or above by 2014. Under NCLB, schools have to meet additional requirements in order to meet AYP. For simplicity, in this report we do not address these other requirements, which include minimum performance on another academic indicator other than test scores—such as graduation rate for high schools; and the requirement of 95% participation on the state assessments.
NCLB Provisions to Support Making Valid and Reliable School Decisions
The NCLB statute and regulations stipulate that states must make reliable and valid decisions regarding whether schools have met AYP or not. The law provides some provisions intended to support making reliable and valid decisions. For example, a school must fail to meet AYP for two years in a row before it is subject to some sanctions; this provision is a partial safeguard against the unreliability caused by any "good class, bad class" fluctuations in the sample of students from one year to the next.
While NCLB specifies that a school must fail to meet AYP two years in a row, NCLB regulations give states the flexibility to make a number of additional decisions that affect the reliability and validity of the state’s version of the accountability system, subject to review and approval by the United States Department of Education. Most states have focused on improving the decision consistency, that is, the reliability of the identification decisions. Two common approaches states have had approved to address concerns about reliability are to use a "minimum cell size" and to use confidence intervals (Marion, White, Carlson, Erpenbach, Rabinowitz, & Sheinker, 2002). Every state has set minimum cell sizes, and approximately 40 states are using confidence intervals. Across the nation, states have set minimum cell sizes that range between 10 and 80 students or more (Forte Fast & Erpenbach, 2004). Some states use a percentage, such as 15% of the enrolled students. In a large high school, this could be the equivalent of a hundred students or more. According to NCLB rules, if a school does not have the minimum number of students for a subgroup calculation, that subgroup is treated as "meeting AYP" for the purposes of determining whether the school met AYP.
In addition to setting a minimum cell size to insure statistical reliability by accounting for year-to-year fluctuations due to sampling error, states may employ a confidence interval to say that a school’s observed performance was truly below the AMO with a specified degree of confidence. The United States Department of Education has approved proposals from a majority of states for either a 95% or 99% confidence interval (Forte Fast & Erpenbach, 2004), meaning that they are willing to accept errors 5% or 1% of the time in stating that a particular subgroup in a school did not meet AYP when it truly did. Since AYP is determined for most schools as a result of multiple decisions, the actual error rate can be considerably more than the nominal 5% or 1% error rate. In practice, states have implemented a one-sided confidence interval that focuses on avoiding identifying schools as not having met AYP if they truly have. If a school’s or subgroup’s observed performance (e.g., percent proficient) falls within the confidence interval or higher, then the school/subgroup is counted as meeting the AMO.
On the other hand, for a variety of reasons states have not attended to the validity requirements to the same extent as they have for reliability issues (Marion & Gong, 2003). Separating reliability and validity, as many measurement professionals have been telling us for a long time, is a false distinction. Many of the so-called reliability solutions such as raising the minimum-n have considerable validity implications. In general, accountability system validity focuses on the accuracy of the identification of schools (i.e., are the "right" schools being labeled as passing or failing?), the consequences—both positive and unintended negative—of the accountability system, and the subsequent interventions as a result of identifying schools (Marion & Gong, 2003). One of these validity implications is central to this report: the consequences for special education students as a result of being included or excluded in the accountability system.
Focus on Students With Disabilities
Special education students are an important subgroup educationally and for school assessment and accountability systems. This was true prior to NCLB, especially with the advent of IDEA 1997, and the NCLB law mentions students with disabilities specifically as one of the subgroups for which schools are to be held accountable. NCLB has caused intense discussion around issues of how appropriately to assess students with disabilities and include them in the accountability system. Students with disabilities have become very practically and politically significant in the early years of NCLB implementation. Many states are suggesting that a high proportion of schools are not meeting AYP because students with disabilities tend to contribute to schools’ failure to meet AYP at a substantial rate. One view is that this finding is accurate and valid—in fact, the performance of students with disabilities is substantially lower than other subgroups. Nevertheless, many state leaders have, for a variety of reasons, expressed concern about the potentially high number of schools identified as not meeting AYP. Among other strategies, this has resulted in states searching for ways to decrease the potential impact of the students with disabilities subgroup on AYP determinations.
One method being employed to reduce the impact of subgroups on school identification has been increasing the minimum cell size, either in general or for the special education subgroup specifically. Increasing numbers of states are also using confidence intervals and seeking to increase the width of the confidence bands (e.g., from 95% to 99%). Although states’ concern with potential over-identification of schools is understandable, if a substantial number of schools are meeting AYP but doing so without actually including their special education subgroup in the calculations, the intention of the law is being circumvented, and students may not be receiving needed attention.
Focus of Study and Analysis Methods
This study addresses three questions:
To address these questions, a small set of analyses on hypothetical confidence interval and cell-size combinations was conducted on actual achievement data from a small, but varied set of states. The study used a single year of elementary/middle school mathematics and reading achievement test data from five states. Either 2003 or 2004 data were analyzed, depending on availability and other factors, such as the stability of the state’s accountability policies.
Student-level achievement data for reading and mathematics were analyzed for each state. Each student was declared proficient or not proficient in reading and mathematics according to that state’s rules. (Appendix A gives details of each state’s proficiency levels and mathematics and reading achievement scales.) The percent of students proficient was calculated for each school in math and reading, for both all the students (assessed) in the school (referred to as the school-as-a-whole) and for the special education students (assessed) in the school. A school was deemed meeting AYP if the percents proficient for reading and mathematics exceeded a given state’s AMOs for both reading and mathematics for the school-as-a-whole and for the special education students or if the percents proficient in reading and mathematics exceeded the state’s AMOs for reading and mathematics for the entire participant pool, and the special education subgroup did not meet the minimum cell size for inclusion in the calculations. This study did not try to replicate the states’ actual final AYP results, which would involve complex inclusion rules, consideration of academic indicators other than test scores, participation rates, and other elements, especially appeals, required by NCLB and that vary across the states.
Passing rates were calculated for minimum cell sizes of 10, 20, 30, 60, 80, and 100 students. Additionally, passing rates were calculated for each of these cell sizes when the AMO was adjusted to reflect a 75, 90, 95, and 99 percent confidence interval.
Basic information about schools and students in the five states’ data sets is shown in Table 1. Of the five states, three are small and the other two are moderate size (approximately 50,000 students tested per grade level). Two states included every grade level in their accountability tests (states 4 and 5). The proportion of testing participants in grades 3–8 who were special education students ranged from a low of approximately 11 percent to a high of approximately 20 percent. This range bracketed the national average of approximately 12% special education students. The average number of students per school in grades 3–8 ranged from fewer than 20 to more than 300.
Table 1. Basic Information on States Included in Analysis
|
State |
Region |
Year |
Number of Tested Students in Grades 3–8 |
Percent of Tested Students in Special Education |
Average Number of Tested Students per School (Standard Deviation Shown in Parentheses) |
Grade Levels Included in Accountability Calculations (Elementary and/or Middle Schools) |
|
1 |
Northeast |
2003 |
25,857 |
20.0% |
92.4 (18.2) |
04, 08 |
|
2 |
Southeast |
2003 |
114,165 |
14.6% |
88.8 (12.9) |
04, 08 |
|
3 |
Northwest |
2004 |
129,471 |
11.5% |
117.1 (84.9) |
03, 05, 08 |
|
4 |
Northwest |
2003 |
61,816 |
13.7% |
18.9 (24.2) |
03–08 |
|
5 |
West |
2003 |
222,484 |
11.0% |
307.7 (237.0) |
03–08 |
The AMOs for the five states represented a large range—36 percentage points between the lowest and highest AMOs in reading and 32 percentage points in math (see Table 2). The lowest AMO in reading was 40% and the highest was 76%. In general, the math AMOs were lower than reading, but exhibited a similar range of differences across the five states, with the lowest math AMO equal to 30% and the highest equal to 62%. The states ranked the same for reading and math AMOs (i.e., a state with a relatively lower AMO in reading had a relatively lower AMO in math), with one exception: State 1’s middle school math AMO was lower compared to the other states relative to its ranking based on reading AMOs. The AMOs were determined by each state according to the percent of students proficient in the school containing that state’s "20th percentile student," following a specific methodology mandated by NCLB (PL 107–110, Section 1111). One state (State 1) used index scores ranging from 0–100 to express school performance, rather than a percent proficient. This state’s AMOs were also expressed on this scale.
Table 2. Annual Measurable Objectives (AMOs) for Elementary and
Middle Schools
in Each State (Percent Proficient Unless Otherwise Stated)
|
State |
Year |
Reading |
Mathematics |
|
1* |
2003 |
76.1 (elementary schools) e68.0 (middle schools) m |
61.7 (elementary schools) e46.1 (middle schools) m |
|
2 |
2003 |
40% |
30% |
|
3 |
2004 |
40% |
39% |
|
4 |
2003 |
64% |
55% |
|
5 |
2003 |
65% |
57% |
* State 1 employed school performance scores on a 0–100
metric for each school. Additionally, the state created separate AMOs for
elementary and middle schools.
e Mean school performance "index score" for elementary schools.
m Mean school performance "index score" for middle schools.
Table 3 shows the percent of students proficient in ELA and Mathematics by special education status for each of the five states.
Table 3. Percent of Students Proficient or Mean School
Performance Score in Reading
and Math for School-as-a-Whole and for Special Education Subgroup
|
State |
Year |
School-As-A-Whole |
Special Education |
||
|
ELA |
Mathematics |
ELA |
Mathematics |
||
|
1 |
2003 |
90.6 (17.1)e 86.0 (18.6)m |
90.2 (16.7)e 84.9 (20.6)m |
79.5 (21.8)e 72.0 (21.4)m |
81.5(21.0)e 69.8 (23.4)m |
|
2 |
2003 |
58.6 % |
57.1 % |
25.5 % |
28.6 % |
|
3 |
2004 |
71.0 % |
69.8 % |
33.3 % |
37.1 % |
|
4 |
2003 |
70.4 % |
65.4 % |
34.6 % |
30.0 % |
|
5 |
2003 |
76.8 % |
71.4 % |
33.7 % |
33.8 % |
e
Mean school performance "index score" for elementary schools.Results—Analyses of Actual Data
School Identification Rates as a Result of the Special Education Subgroup
The first set of analyses examined the simple descriptive statistics comparing the percentage of schools that meet the AMOs for the school-as-a-whole subgroup and for the special education subgroup (see Table 4) (we acknowledge that it seems ironic to call the "school-as-a-whole" a subgroup, but that is a specific NCLB defined subgroup). Notably, the pass rate for schools with regard to special education is quite low compared to the school-as-a-whole. In other words, the performance of the special education subgroup will lead to schools’ failure at a noticeably higher rate than for the school-as-a-whole. The final column of Table 4 shows the percentage of schools reaching AMOs for the student body-as-a-whole, but lacking sufficient cell sizes to assess the progress of special education students. Several details of this table bear mentioning. In the five states studied, over 80 percent of schools that passed their subgroup AMO did so without assessing the proficiency of their special education students. An additional finding from these analyses is the variability in passing rates (minimum approximately 46%, maximum approximately 92%). The two states with the lowest passing rates (States 4 and 5) are the two states currently testing every grade. Again, these results are aggregated across all minimum cell sizes and confidence intervals.
Table 4. Percent of Schools Meeting AMOs for Particular Student Subgroups Across All Experimental Conditions
|
State |
Passed: School-as-a-Whole (Percent of Schools) |
Passed: Special Education (Percent of Schools) |
Passed* (Percent of schools) |
Percent of Total Schools that Passed but Lacked the Minimum-n in Special Education |
|
1- (n = 277) |
96.8 % |
75.3 % |
92.2 % |
82.7 % |
|
2- (n = 1283) |
86.8% |
34.2 % |
79.4 % |
94.0 % |
|
3- (n = 1112) |
95.9 % |
49.3 % |
87.9 % |
90.4 % |
|
4- (n = 440) |
61.8 % |
13.6 % |
46.5% |
93.5 % |
|
5- (n = 723) |
78.8 % |
10.1 % |
50.9 % |
92.1 % |
*Passed both components or passed school-as-a-whole but lacked
minimum-n in special education.
The Effect of Minimum-n
The number of students required to define a set of students as a group has been one of the most discussed aspects of states’ implementation of AYP calculations. It has been argued previously (e.g., Marion, et al., 2002) that minimum-n is much less of a reliability issue than a consequential validity concern. The analyses presented in Table 5 document the effects, while holding all other aspects of states’ accountability plans constant, of altering the minimum number of students necessary to constitute a subgroup on the percent of schools passing AMOs for each of the five states. As one would expect, an increase in the minimum cell size was associated with an increase in the percentage of schools passing AMOs. All but one state (State 1) showed a difference of more than 25 percentage points. Perhaps this is due to this state’s having "less room" for change.
Table 5. Percent of Schools Meeting AMOs by Minimum Cell Size
|
State |
Minimum Cell Size |
|||||
|
10 |
20 |
30 |
60 |
80 |
100 |
|
|
1 |
83.0% |
88.9% |
92.1% |
95.6% |
96.8% |
96.8% |
|
2 |
58.0% |
75.7% |
82.4% |
86.7% |
86.7% |
86.8% |
|
3 |
68.6% |
81.1% |
90.1% |
95.7% |
95.9% |
95.9% |
|
4 |
28.4% |
35.4% |
41.3% |
56.6% |
57.9% |
59.7% |
|
5 |
18.6% |
26.5% |
40.0% |
70.1% |
74.0% |
75.8% |
Consequences of Increasing Minimum-n
Two analyses were conducted to examine the consequences on special education students of increasing the minimum-n. The first demonstrates quite conclusively for these states that as the cell size requirements increase, fewer schools are held accountable for ensuring that their special education students meet the AMOs. Table 6 shows, for each minimum cell size, the percentage of schools passing their AMOs but without sufficient numbers of special education students to assess their performance. When minimum cell sizes approached 60, almost 100 percent of schools in all five states were able to "pass" AYP without the performance of special education students taken into account.
Table 6. Percent of Passing Schools Not Having Enough Special Education Students
to Meet Minimum Cell Size Requirements
|
State |
Minimum Cell Size |
|||||
|
10 |
20 |
30 |
60 |
80 |
100 |
|
|
1 |
34.3% |
75.4% |
83.1% |
97.1% |
99.6% |
99.6% |
|
2 |
65.0% |
91.9% |
97.3% |
100.0% |
100.0% |
100.0% |
|
3 |
53.1% |
81.9% |
95.8% |
100.0% |
100.0% |
100.0% |
|
4 |
70.6% |
83.4% |
91.3% |
99.7% |
100.0% |
100.0% |
|
5 |
42.4% |
69.0% |
88.7% |
99.3% |
99.8% |
99.9% |
The second analysis focuses on the percentage of special education students that would be excluded from the accountability system as a function of increasing cell size. We recognize that these students are not fully excluded because they count in the whole school calculations, but practically for most AMO levels, schools could feasibly ignore the performance of special education students until 2011 or so. Table 7 shows the percentage of tested special education students excluded from the AYP calculations for each state and cell size. For the three states not testing every grade, more than one-third of special education students were excluded from AYP calculations at a minimum cell size of 20. For these states, by the point the minimum cell size reached 60 students, nearly 100 percent of special education students were not included in the AYP calculations. This has consequences for special education students and on the validity of the accountability system.
Table 7. Percent of Special Education Testing Participants Excluded By Minimum
Cell Size
|
State |
Minimum Cell Size |
|||||
|
10 |
20 |
30 |
60 |
80 |
100 |
|
|
1 |
10.3% |
38.5% |
49.6% |
86.2% |
97.7% |
97.7% |
|
2 |
18.5% |
54.1% |
75.7% |
98.6% |
98.9% |
100.0% |
|
3 |
10.7% |
41.2% |
73.7% |
99.1% |
100.0% |
100.0% |
|
4 |
8.7% |
20.7% |
31.6% |
72.4% |
79.7% |
87.0% |
|
5 |
1.5% |
6.9% |
20.3% |
67.5% |
79.9% |
87.5% |
The Effect of Confidence Intervals on AYP Pass Rates
One approach that has been advocated for improving the reliability of AYP decisions has been to use confidence intervals around either the AMO or the school’s observed score (e.g., Hill & DePascale, 2003; Marion et al., 2002). In these analyses, the confidence interval was varied while the minimum-n was held constant at the average of the minimum-n values tested earlier. It is a mathematical necessity that passing rates increase with the increasing confidence interval on the target AMO; however, the increase is quite small compared to the results for minimum cell sizes (see Table 8). Appendix B describes the inferential statistical analyses underlying conclusions presented in this report.
Table 8. Percent of Schools Passing AMOs by Confidence Interval Size
|
State |
Confidence Interval Size |
||||
|
NONE |
75 |
90 |
95 |
99 |
|
|
1 |
89.8% |
90.9% |
92.7% |
93.0% |
94.5% |
|
2 |
70.6% |
76.5% |
80.6% |
83.0% |
86.2% |
|
3 |
83.1% |
86.0% |
88.5% |
90.0% |
91.8% |
|
4 |
37.7% |
43.0% |
47.2% |
49.6% |
55.2% |
|
5 |
45.8% |
48.3% |
51.4% |
52.6% |
56.4% |
Projections for Testing Every Grade 3-8
States are required to test every grade, 3–8 and once in high school, by the 2005–2006 school year. Prior to that year, schools were required to test students once each in elementary, middle, and high school. With fewer grades being tested, there are fewer students eligible to meet minimum cell sizes. Further, confidence intervals vary inversely as a function of sample size (i.e., they are wider when sample sizes are smaller). Therefore, if the level of the confidence interval does not change, they will, by definition, be narrower when more students are included in the system. Similarly, with more grades tested, more subgroups will meet the minimum-n threshold (assuming it stays at the same level). The analyses presented in this section project how the various design decisions play out when the full assessment system is implemented.
Three of the five states (States 1, 2 and 3) did not test every grade in recent years. Data from these states’ October, 2004, enumeration of their schools’ enrollments was used to make projections of passing rates likely when every grade, 3–8, is tested. It was assumed that the untested students were sampled from the sample population as tested students and, therefore, the percent proficient for the tested and untested groups was identical. It was also assumed that the proportion of special education students was the same between the tested and untested grades. Each school’s total enrollment, grades 3–8, was used as the participant count for analyses by minimum cell size and as sample size in the calculation of the confidence intervals for the analyses by confidence interval size.
Tables 9 and 10 show projected numbers of students and passing rates for the three sampled states currently testing two or three grades if they were to test every grade in grades three through eight. Table 11 shows the differences in pass rates from partial to every grade testing for these three states. As one would expect, the pass rates for the student body as a whole did not change very much from partial to complete grade testing. However, the overall pass rate decreased between approximately 7–20 percent.
Table 9. Projected Average Number of Testing Participants Per School If Every
Grade Tested.
|
State |
Projected Mean (Standard Deviation) Number of Students Participating in Testing |
Projected Mean (Standard Deviation) Number of Special Education Students Participating in Testing |
|
1- (n = 244) |
294.83 (59.22) |
59.22 (48.11) |
|
2- (n = 1230) |
267.01 (206.12) |
39.02 (30.12) |
|
3- (n = 1012) |
248.63 (210.89) |
29.06 (24.67) |
Table 10. Projected Percent of Schools Passing AMOs for Particular Student
Subgroups Across All Experimental Conditions If Every Grade Tested
|
State |
Passed: School-as-a-Whole (Percent of schools) |
Passed: Special Education (Percent of Schools Meeting Minimum-n) |
Passed* (Percent of All Schools) |
Percent of Total Schools that Passed but Lacked the Minimum-n in Special Education |
|
1- (n = 244) |
98.4 % |
75.4 % |
85.5 % |
51.1 % |
|
2- (n = 1230) |
81.8 % |
31.3 % |
57.5 % |
76.3 % |
|
3- (n = 1012) |
96.2 % |
35.6 % |
76.3 % |
83.9 % |
|
4- (n = 440) * |
61.8 % |
13.6 % |
46.5% |
93.5 % |
|
5- (n = 723) * |
78.8 % |
10.1 % |
50.9 % |
92.1 % |
* Actual data from States 4 and 5 repeated for ease of comparison. "Passing" in this column refers to those subgroups actually meeting the AMO or not having enough students to constitute a subgroup.
Table 11. Projected Difference in Percent of Schools Passing AMOs Across All
Experimental Conditions
|
State |
Passed: School-As-A-Whole (Percent of Schools) |
Passed: Special Education (Percent of Schools Meeting Minimum-n) |
Passed* (Percent of Schools) |
Passed but Lacking Minimum-n in Special Education (Percent of Passing Schools) |
|
1- (n = 277) |
+1.6 % |
-0.1% |
-6.7% |
-31.6% |
|
2- (n = 1283) |
+ 5.0 % |
-2.9% |
-21.9% |
-17.7% |
|
3- (n = 1116) |
+0.3% |
-13.7% |
-11.6% |
-8.2% |
* Passed both components or passed school-as-a-whole but lacked
minimum n in special education.
Effects of Minimum-n with All Grades Testing
As more students are added into the system, more schools will meet the minimum-n thresholds for various subgroups. The pattern of projected percentages of schools passing AYP at varying levels of minimum cell size (see Table 12) is similar to the pattern for testing fewer students (see Table 5), although slightly fewer schools are able to pass with more students included. Even with the additional students included in the system, a majority of the projected passing schools do so without having sufficient numbers of special education to constitute a subgroup once the minimum-n reaches 30 students (see Table 13). Likewise, once the minimum-n reaches 20 or 30 students, significant percentages of special education students are excluded from the accountability system even with all grades tested (see Table 14). Figures 1–3 show the exclusion rates for the three states without a full assessment system now compared with the exclusion rates when the system is fully built out as a function of cell size.
Table 12. Projected Percent of Schools Passing AMOs by Minimum Cell Size If Every Grade Tested
|
State |
Minimum Cell Size |
|||||
|
10 |
20 |
30 |
60 |
80 |
100 |
|
|
1 |
76.4% |
77.7% |
81.7% |
89.1% |
93.7% |
94.7% |
|
2 |
33.4% |
40.6% |
50.3% |
68.7% |
74.3% |
77.7% |
|
3 |
49.6% |
58.7% |
73.2% |
86.4% |
90.3% |
93.7% |
|
4* |
28.4% |
35.4% |
41.3% |
56.6% |
57.9% |
59.7% |
|
5* |
18.6% |
26.5% |
40.0% |
70.1% |
74.0% |
75.8% |
* Actual data from States 4 and 5 repeated for ease of comparison.
Table 13. Projected Percent of Passing Schools Not Meeting Minimum Cell Size Requirements for Special Education Students If Every Grade Tested
|
State |
Minimum Cell Size |
|||||
|
10 |
20 |
30 |
60 |
80 |
100 |
|
|
1 |
1% |
7.4% |
35.1% |
77.7% |
82.3% |
85.4% |
|
2 |
8.4% |
36.7% |
64.6% |
93.9% |
96.8% |
98.6% |
|
3 |
26.6% |
57.5% |
86.4% |
99.1% |
99.5% |
99.9% |
|
4* |
70.6% |
83.4% |
91.3% |
99.7% |
100.0% |
100.0% |
|
5* |
42.4% |
69.0% |
88.7% |
99.3% |
99.8% |
99.9% |
* Actual data from States 4 and 5 repeated for ease of comparison.
Table 14. Projected Percent of Special Education Students Excluded By Minimum Cell Size If Every Grade Tested
|
State |
Minimum Cell Size |
|||||
|
10 |
20 |
30 |
60 |
80 |
100 |
|
|
1 |
< 1% |
1.4% |
11.3% |
40.1% |
49.7% |
55.4% |
|
2 |
1% |
6.4% |
18.9% |
55.7% |
70.6% |
81.8% |
|
3 |
2.7% |
13.0% |
37.5% |
67.5% |
77.8% |
88.7% |
|
4* |
8.7% |
20.7% |
31.6% |
72.4% |
79.7% |
87.0% |
|
5* |
1.5% |
6.9% |
20.3% |
67.5% |
79.9% |
87.5% |
* Actual data from States 4 and 5 repeated for ease of comparison.
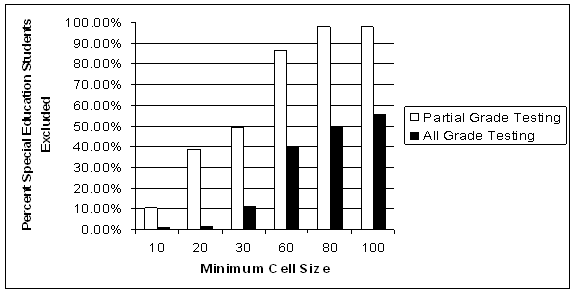
Figure 1. State 1: Percent Special Education Students Excluded: Partial Grade Testing Versus Projected All Grades Testing

Figure 2. State 2: Percent Special Education Students Excluded: Partial Grade Testing Versus Projected All Grades Testing
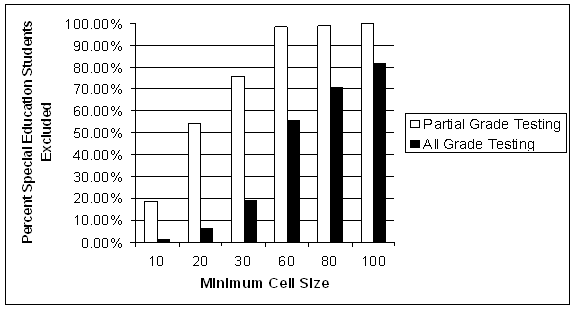
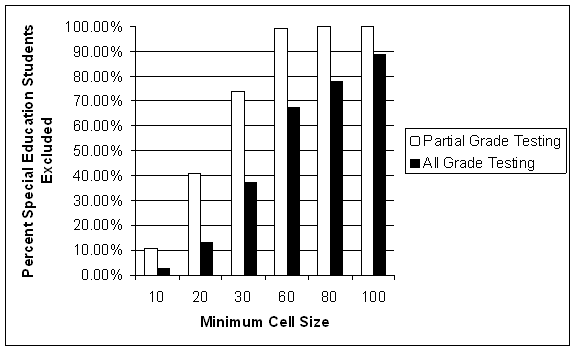
Figure 3. State 3: Percent Special Education Students Excluded: Partial Grade Testing Versus Projected All Grades Testing
Effects of Confidence Intervals with All Grades Testing
When more students are added into the system, the width of the confidence interval bands will decrease. The general pattern found for all grades testing were similar to those from the analyses for partial grade testing (see Table 15).
Table 15. Percent of Schools Passing AMOs by Confidence Interval Size If Every Grade Tested
|
State |
Confidence Interval Size |
||||
|
NONE |
75 |
90 |
95 |
99 |
|
|
1 |
81.2% |
84.9% |
86.5% |
86.9% |
88.1% |
|
2 |
50.0% |
54.4% |
58.2% |
60.4% |
64.4% |
|
3 |
70.5% |
73.2% |
75.8% |
77.1% |
80.0% |
Summary and Conclusions
While states have flexibility in meeting the NCLB reliability expectations, their choices can lead to severe consequences for special education students. Most troublesome is the application of high minimum-n requirements. When the minimum-n was simulated to equal 60 students (well within the range of state values), more than half of the special education students in four of the five states—even when projecting all grades testing—were excluded as an explicit subgroup from the accountability system.
Increases in minimum cell sizes for the special education subgroup were associated with a large increase in passing rates for each of the five states assessed. This increase was due, in large part, to schools being less likely to have to include the results for the special education subgroup as the minimum cell size increased. In line with earlier predictions (Marion, 2004), it is considerably easier for a school to meet its AMO without reporting the proficiency of their special education students. Increased confidence interval sizes were also associated with an increase in pass rates, but a much smaller increase. While raising the minimum-n is an effective means of increasing the passing rates of schools, it does so at a considerable cost to special education students in terms of being excluded from the accountability system. If the implicit theory of action guiding NCLB accountability requirements is to improve instruction and thus outcomes for all students, schools and districts must be accountable for all subgroups in order to ensure that these students are appropriately served. The effect of increasing the minimum-n to exclude substantial portions of special education students must be considered a threat to the validity of the accountability system.
Many more special education students’ data are reflected in the accountability results when all grades are tested. This assumes that states will not increase the minimum-n as more grades are tested. If they do so, then it will likely be a wash between the increase in available students and the loss of these students through increases in required cell sizes.
Although confidence intervals have been suggested as a means of increasing the reliability of school identifications as well as reducing the number of schools failing to make AYP (i.e., because it will reduce those falsely identified), the data presented in this study suggests that confidence intervals have a much smaller impact on AYP pass rates than minimum-n changes. One of the reasons for this finding is the relatively large difference between the observed performance of the special education subgroup and the performance targets in the five states. Three of the five states had relatively high AMOs (e.g., > 60% proficient). If only a small proportion of special education students are scoring proficient, then the confidence intervals will still not be wide enough to overlap the AMO. In other words, if the difference between the percent of special education students scoring proficient and the AMO is large, confidence intervals will still not "help," assuming the motive for adjustment is to reduce numbers of schools identified as not meeting AYP. In only one of the five states did more than 50 percent of the schools have their special education subgroup meet the state’s AMOs.
Confidence intervals will not help the special education subgroup pass when they should really not pass (i.e., they are far below the AMO), but can help the state leaders make this decision more reliability. On the other hand, minimum-n approaches do little to improve the reliability of subgroup decisions (at least within the range of minimum-n levels being used by most states), but can have severe negative consequences for subgroups excluded and, by extension, threaten the validity of the accountability system.
References
Forte Fast, E., & Erpenbach, W. J. (2004). Revisiting statewide educational accountability under NCLB: A summary of requests in 2003–2004 for amendments to state accountability plans. Washington, D.C.: Council of Chief State Schools Officers.
Hill, R.K., & DePascale, C.A. (2003). Reliability of No Child Left Behind accountability designs. Educational Measurement: Issues and Practice, 22(3), 12-20.
Marion, S. F., White, C., Carlson, D., Erpenbach, W. J., Rabinowitz, S., & Sheinker, J. (2002). Making valid and reliable decisions in the determination of adequate yearly progress: A paper in the series: Implementing the state accountability system requirements under the No Child Left Behind act of 2001. Washington, D.C.: Council of Chief State Schools Officers.
Marion, S. (2004). An analysis of differential rates of states’ identifying schools as "not meeting AYP" in 2003 under the federal No Child Left Behind law. Dover, NH: National Center for the Improvement of Educational Assessment.
Marion, S. F., & Gong, B. (2003). Evaluating the validity of states’ accountability systems. Paper presented at the Reidy Interactive Lecture Series. October 9–10. Nashua, NH.
P. L. 107–110 ‘‘No Child Left Behind Act of 2001,’’ Title I-Improving the Academic Achievement of the Disadvantaged, Section 1111.
Appendix A
Details of Each State’s Proficiency Scoring for Mathematics and Reading
|
State |
Number of Points on Proficiency Scale |
Mastery Determination |
Notes |
|
1 |
Six points [0,1,2,3,4,5] converted to five index levels [0,25,50,75,100]. |
A student’s score is equal to 5. |
A school meets AYP if its index score is greater than AMO index score. |
|
2 |
Five points [1,2,3,4,5] |
A student’s proficiency score is greater than or equal to 3. |
|
|
3 |
Five points [1,2,3,4,5] |
A student’s proficiency score is greater than or equal to 4. |
This state reports scores for basic reading, reading, writing, mathematics skills, concepts and problem solving. For the current study, the basic reading and mathematics skills proficiency scores were used. |
|
4 |
Four points [1,2,3,4] |
A student’s proficiency score is greater than or equal to 3. |
|
|
5 |
Four points [1,2,3,4] |
A student’s proficiency score is greater than or equal to 3. |
The mathematics test for grades 7–8 may cover algebra, geometry, or pre-algebra depending on the student’s curriculum. In the current study, a student’s score was included regardless of curriculum. |
Appendix B
Inferential Statistical Analyses Conducted for this Report
Separate repeated measures logistic regressions were conducted for each of the five state’s passage determinations. SAS, version 8.02, proc GENMOD was used (SAS Institute, 2001). The independent variables were minimum cell size and confidence interval size. The logistic regression function in these analyses describes the probability of a school failing. Regression coefficients in the current analyses describe the degree of association between increasing values of the predictor variables with the probability of failing. Cell size and confidence interval size were dummy-coded into a set of dichotomous variables comparing the probability of being declared non-proficient in the very highest level of the variable with that in the other levels. For instance, in one state’s data, the logistic regression coefficient for a minimum cell size of 10 was 1.82 (.18), Z = 10.36, p < .0001. This coefficient indicates that a school using a minimum cell size of 10 was approximately 6 times more likely to be declared failing than a school with a minimum cell size of 100 special education students.
Regression coefficients comparing the lower minimum cell sizes with the highest minimum cell sizes were always significantly different from 0. On the other hand, when regression coefficients for comparing the widest confidence interval sizes with other confidence interval sizes were significant, it was usually only for the narrowest confidence intervals, and these coefficients were always smaller than those comparing cell sizes. When regression coefficients for the combinations of cell size and confidence interval size were significant, it was only for the combinations of lowest cell sizes and narrowest confidence intervals. This interaction effect was, however, of little substantive interest. The interaction between cell size and confidence interval size could not be assessed for State 1’s original data, most likely because of collinearity. Results were similar for the analyses conducted with projected cell sizes.